The following is to be done as one program and not a series of small programs. Please note that no operation is to corrupt the structure of the tree. It should be possible to run any traversal in any order, repeatedly.

Data set for the assignment is given in the file ass2.dat.

1. Using the data from the data file (ass2.dat) create a tree which adheres to the Binary Search Tree structure.  Each name in the data set should account for a separate node (which will be referred to as a name node) in the tree. While the tree is being created, thread the tree so a symmetric order traversal is possible.
2. Write a recursive pre-order, inorder and post-order traversal, and print out the results of these traversals. Be sure to account for the threads.
   
3. Implement a symmetric order traversal using threads. These are the threads you have created in part a.
4. Using a traversal of your choice, scan the tree, and for each word node encountered, build a second B.S.T. (character tree) which will hold the characters of the name. This second B.S.T. will be pointed to from the encountered name node. Each node in this tree will be composed of a character of the encountered name plus the number of times the character occurred in the name. Note: the comma , blanks and other none alpha characters should be filtered out. As the word is scanned, each character is inserted into the character tree, if the character encountered is not in the tree then it is added at the appropriate point. If the character already exists in the tree, then a counter within the node is incremented. For example, a name  node (name  is SMITH, MATT P) with an associated character tree will look as follows. Treat upper case and lower case characters the same.
   
 

 
 

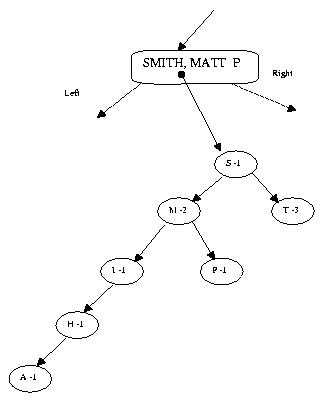
The short hand notation S-1 indicates that the character S occurs once in the word SMITH, MATT P.
 


5. Print out an alphabetical list of the names in the tree. As each name is printed, output an alphabetical list of the characters of the name and the number of times each character appears in the name.
6. From the handout given in class, implement a S.O.T. using iteration to traverse the character tree.  Show that this implementation works by printing out a second alphabetical list of the names in the tree as in  part e, and the associated character tree. They should be the same.
   

7. Using the same tree, generate the output as in part e except this time, use the link inversion algorithm to traverse the character tree.
8. To ensure that the link inversion algorithm did not corrupt the tree, repeat part e.

Notes:

Part b is simple, code given in class, be sure to account for the threads.

Part c was given in class, type it in and let it run.

Part d is simpler then it looks. Each name node will have an additional pointer, which points to the root node of the character tree. The code for the character tree is a standard BST insert. For each BST insert you may use the iterative or recursive method, which ever you find easier. I find the recursive method easier, but that is personnel preference.

Part e is verifying that everything up to now is still OK. Scan the name tree and the subtrees; and dump out a list as specified.

Part f is the hard part, the code can be a little cryptic to go over, I expect most of your sleepless nights will be spent on this section

Part g and h are bonus and should not be attempted unless you have everything else working. The link inversion algorithm, although given, must be translated into java code devoid of go to statements. There are two popular methods to implement this algorithm. Using a case statement inside a loop, or a few labelled loops with labelled break and continue statements. Since this is bonus, you are free to use which ever method you like.

Output governed by the recursive SOT is designed to ensure you do not corrupt your tree. As long a it can be read then OK. If you want to dump the traversal on 1 long line with a little spacing that is ok. Remember, we do need to read it, so a little neatness is desired. Saving trees might also be a consideration.

Allot of code exists in the book. You may be tempted to copy this code and then hope to get it working. I have never seen much luck with this method, especially when the problem deviates from the example solutions. Think about what you need to do, and then devise an algorithm to attack the problem. Standard algorithms like BST inserts can be copied, but you may find it difficult to directly modify existing binary tree code to accommodate the requirements given here. Think before you type!
 

Submission Requirements:

• Cover Sheet completely filled out, available from: "http://www.cosc.brocku.ca/forms/cover" Note: your assignment will not be marked unless one is submitted with the assignment on the assignment due date.
• Commented and properly documented source code listing, use Java Doc style.
• Listing of any input you used to test your program.
• Listing of your output which reflects the input.
• Source code is to be Java.
• Electronic submission, run the script "submit2p03" from sandcastle.
• Statement on coversheet with following information.
• Platform, e.g. Mac, PC, Commodor 64, my Java enabled wrist watch.
• Compiler Version, e.g. Java 1.7, Java 1.81 e.g.